고등 수학 (상) 켤레복소수와 복소수의 사칙연산

안녕하세요 이번 포스팅에서는 켤레복소수와 복소수의 사칙연산에 대해서 알아보도록 하겠습니다.

 

켤레복소수

켤레복소수에 대해 알아보기 전에 간단히 알려주자면 저번 포스팅에서 배운 복소수 a+bi에서 a는 실수 부분, b는 허수 부분이라고 배웠습니다. (자세한 내용은 링크 타고 가시면 복소수의 기본개념 글이 있습니다.)

 

켤레복소수란 복소수 a+bi (a, b는 실수)에 대해 허수 부분의 부호를 바꾼 것인 a-bi입니다.

이것을 기호로 나타내면 아래 사진처럼 a+bi 위에 선을 그어서 나타냅니다.

복소수는 보통 z라고 표시합니다. 즉 z = a+bi인 것이죠.

복소수 z의 켤레복소수는 z 위에 선을 그은 것으로 나타낼 수 있고 읽을 때는 "z bar"라고 읽습니다.

 

또한 복소수 z가 실수이면

복소수 z가 순허수이면

 

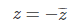
켤레복소수의 성질

켤레복소수의 성질을 좀 더 잘 이해하기 위해서는 복소수의 사칙연산에 대해서 알아야 하기 때문에

복소수의 사칙연산에 대해 배워보도록 하겠습니다.

 

복소수의 사칙연산

복소수의 덧셈과 뺄셈은 허수단위인 i를 문자처럼 생각하여 실수부분은 실수 부분끼리, 허수 부분은 허수 부분끼리 계산해야 합니다.

 

a, b, c, d가 실수일 때 아래와 같이 계산할 수 있습니다.

 

복소수의 곱셈은 다음과 같이 분배법칙을 이용해 전개한 후 i²=-1 임을 이용해 계산합니다.

a, b, c, d가 실수일 때

 

복소수의 나눗셈은 분모의 켤레복소수를 분모, 분자에 각각 곱하여 계산합니다. 이를 분모의 실수화라고 합니다

a, b, c, d가 실수 일 때

 

복소수의 사칙연산의 성질

복소수도 실수와 마찬가지로 다음과 같이 교환, 결합, 분배법칙이 작용합니다.

세 복소수 z₁, z₂, z₃에 대하여